Magpie Bridge

二体运动

两个质量不等的粒子,各自绕共同质心公转。

两个质量相当的粒子,依循各自椭圆轨道,绕着质心公转。
一个稳定三体系统列子(视频)
地球静止轨道卫星
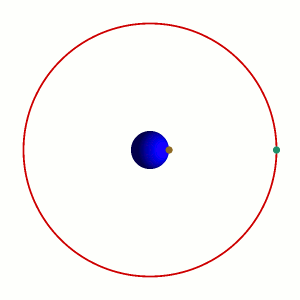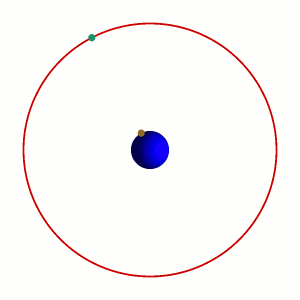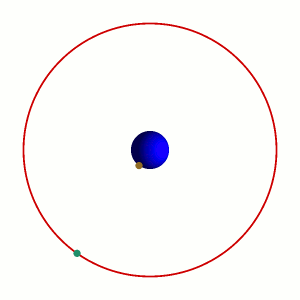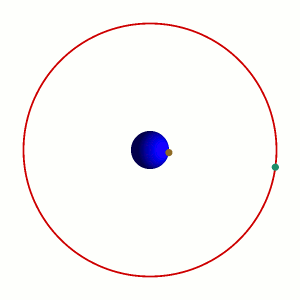
卫星绕地球旋转角速度等于地球自转角速度
利用行星引力变速

gravity assists to alter the path and speed of a spacecraft
利用行星引力进行减速

gravity assists to alter the path and speed of a spacecraft
利用行星引力进行加速
美国卫星全球定位系统(GPS)
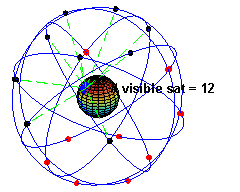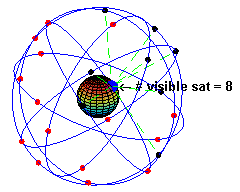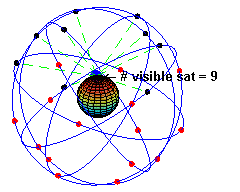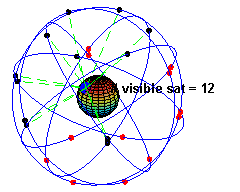
月球背面探测和“鹊桥”中继卫星


白色为 “鹊桥”中继卫星,绿色为“嫦娥四号”探测器
轨道力学(视频)
轨道力学(Orbital mechanics)
轨道力学以各类航天器为研究对象,分析它们在万有引力及其它外力作用下的运动特性及控制规律。研究过程中,一般把航天器抽象为质点或质点系力学模型,轨道力学的研究内容可分为轨道动力学和轨道控制两部分。
* 轨道力学演变
当古人仰望诸天从诸神那里寻求指导时,他注意到星型并开始记录它们在诸天上的运动。 古人认为地球是平坦的。 但是在公元前350年左右,古希腊亚里斯多德证明了地球是圆形的。 以后在大约公元150年,克劳狄乌斯·托勒密(约90年—168年)提出了地心说理论,即地球静止在宇宙的中心,太阳、月亮、星星和行星围绕地球在复杂的轨道上旋转。 在1500年代, 波兰的尼古拉·哥白尼提出了日心说理论,认为地球绕太阳公转,并绕其地轴旋转。这方面天文学演变成复杂的行星运动研究称为轨道力学。 如今,轨道力学已应用于太空飞行和卫星,这些卫星绕地球轨道或在太阳系外飞行。
* 开普勒行星运动三定律
1600年代初期,德国数学家约翰·开普勒(Johann Kepler)利用丹麦科学家第谷·布拉赫(Tycho Brahe)收集的行星观测数据,开发了三个行星运动定律。
开普勒第一定律规定,所有行星都在椭圆轨道上运动,在椭圆的一个焦点上有太阳,而在另一个焦点上是空的。 应用于地球卫星时,地心成为一个焦点,另一个焦点为空;对圆形轨道,两个焦点重合。
开普勒第二定律(面积定律): 连接行星与太阳的连线在相等的时间间隔内扫过相等的面积。当卫星沿轨道运动时,连接行星与太阳的连线在相等的时间段内扫过相等的面积。如果面积一、二和三相等,时间一、二和三也相等。因此,卫星的速度随其离地球中心的距离而变化
轨道上速度最大、离地球最近的点称为近地点(Perigee) ;速度最小、离地球最远的点称为远地点(Apogee)。 着重注意的是,卫星运行的轨道与质量无关。 一颗大而重的卫星可以和一颗小而轻的卫星在同一轨道上运行,两者都在相同的时间段内扫过相等的面积。
开普勒第三定律,周期定律:它关系行星绕太阳运行一圈所需的时间与其离太阳的平均距离。 对于任何行星,其旋转周期的平方都与它与太阳的平均距离的立方成正比。 应用于地球卫星,开普勒的第三定律解释说,卫星离地球越远,完成轨道所需的时间就越长,完成轨道所需的距离也就越大,其平均速度也会越慢。
古典力学之父艾萨克·牛顿为轨道力学奠定了基础,他结合开普勒和其他学者的工作推导了万有引力定律和牛顿运动三定律。开普勒定律提供了轨道运动的概念模型,而牛顿定律为轨道的数学描述奠定了基础,它们解释了卫星为何停留在轨道上的原因。
* 牛顿万有引力定律
牛顿万有引力定律:宇宙中的任何两个物体(例如地球和月球)都以与它们的质量乘积成正比且与它们之间的距离的平方成反比的力相互吸引,简而言之,就是物体质量越大,或相互间距离越近,则引力越大。
* 牛顿运动三定律
牛顿第一运动定律:除非有外力作用,否则运动中的物体将保持相同的速度和相同的方向运动。 卫星以弯曲的路径绕地球运动,因为地球的引力是对其施加的外力。
牛顿的第二运动定律, 如果作用在物体上的合力之和不为零,则物体将具有与合力大小成正比且沿合力方向的加速度。 牛顿第二定律指出,力等于质量乘加速度,正是这个数学方程和万有引力方程构成了轨道计算的基础
F=ma
牛顿的第三运动定律解释了卫星是如何从每一个作用有大小相等方向相反的反作用进入轨道的。 如果你吹大一个气球然后放开它,则气球被喷出的空气作用向前推动。火箭喷出燃气就像空气从气球中喷出一样。
下面说明卫星如何停留在轨道上。 如果一个人站在山上并向水平方向发射弹丸,那么重力将使弹丸的路径向下弯曲并撞击地球。 但是,如果该人以足够快地特定度发射弹丸,由于重力,弹丸路径的曲率将与其下方的地球曲率相匹配。 然后,弹丸将绕地球行进,成为绕地球轨道运行的卫星。
如果弹丸发射速度更快,则弹丸飞行路径将远离地球,但是重力将起作用使弹丸减速,改变其飞行路径并将其拉回地球。如果弹丸速度增加到足以逃脱地球引力,该速度称为逃逸速度,在地球表面, 它约等于7 英里每秒。前面的描述没有考虑大气阻力和地球自转,这两者都会影响弹丸的轨迹。这里阐述了控制卫星轨道的原理。
*地心赤道坐标系和轨道六要素
在空间对轨道进行定向时,必须定义三维坐标系。常用的坐标系是地心赤道坐标 系,其原点位于地球中心。该坐标系是一个非旋转参考系统,在该系统中,卫星轨道平面相对于恒星保持固定,而地球在该坐标系下面转动。 该坐标系的XY平面是地球的赤道平面, x轴正向指向春分点,这是每年春季的第一天,是太阳向北穿过地球赤道的点。Z轴沿着地球的自转轴线朝向北极。

地心赤道坐标系
有六个轨道元素,它们规定了轨道在空间的大小、形状、方向、以及航天器在轨道上的位置。基于椭圆轨道,六个轨道元素是半主轴的长度(a),偏心距(e),倾角(i),升交点赤经(Ω),近地点角距(ω),通过近地点的时间(t0)。
椭圆轨道的主轴线是近地点和远地点的连线。第一个轨道元素是半主轴的长度(a),它是主轴线的半长度。圆轨道没有远地点(Apogee)或近地点(Perigee),因此半主轴(a)为轨道直径的1/2。半主轴用于定义轨道的大小,由此可以计算出卫星运行一个轨道所花费的轨道周期或时间。
轨道的形状由称为偏心率(e)的第二轨道元素定义。对于所有椭圆轨道,偏心率的值在0到1之间,偏心率越大,轨道越椭圆。当 绕地球轨道运行的航天器的偏心率等于或大于1时,它将逃离地球的引力场。
交点是卫星轨道与地球赤道平面的交点,升交点是航天器轨道从南向北与地球赤道的交点; 降交点是航天器从北向南穿过赤道的交点,连接这两个交点的线称为交点线。
轨道的方位由三个轨道元素角确定,升交点赤经(Ω是x轴与升交点之间的夹角,它始终是从地球赤道平面中远离春分点的方向向东测量。近地点幅角(ω) 是升交点与近地点之间的夹角,该角度是在航天器运动方向沿轨道平面测量。 倾角(i)是赤道平面和轨道平面之间的夹角。
上述五个轨道要素描述了空间轨道的大小、形状和方位。 最后一个元素是时间,用于卫星在其轨道上的定位。 卫星以一种非常可预测的方式运动,它按计划运行,因此如果知道卫星经过某个特定点的时间,则可以确定它经过任何其他点的时间,所选的特定点是近地点,近地点通过的时间是六个轨道元素中的最后一个。 六个轨道元素 描绘了在非旋转坐标系中航天器的轨道。
*地心轨道坐标系和二体运动方程解

地心轨道坐标系
图中:
r表示卫星相对于地心的位置矢量,r表示位置矢量的幅值大小;
v表示卫星相对于地心的速度矢量,v表示速度矢量的幅值大小;
Φ表示飞行角,又称航迹角,是速度矢量和垂直于位置矢量的直线之间的夹角;
a表示椭圆的半长轴;
b表示椭圆的半短轴;
c表示轨道中心到一个焦点的距离;
θ表示椭圆的真近点角,又称极角,即地心到近地点的矢量与卫星位置矢量之间的夹角,沿运动方向度量;
ra 表示地心到椭圆轨道上最远点A(远地点)的距离;
rp表示地心到椭圆轨道上最近点P(近地点)的距离;
e表示椭圆偏心率,e = c/a。
二体运动方程解析解为

式中:a是半长轴,e是偏心率,θ是真近点角。当a、e各取为定值时,r仅是 θ的函数。
由解析几何学知识可知,上述解式是圆锥截线的极方程,它给出卫星位置矢量r的幅值r 随a、e、θ值得变化。
* 顺行轨道、 极轨道、逆行轨道
在升交点处具有向东速度分量的卫星的轨道倾角在0到90度之间,这种轨道称为顺行轨道;卫星在升交点处向北移动的卫星处极轨道中,极轨道的轨道倾角恰好为90度;在升交点处具有向西速度分量的卫星是在逆行轨道中,且轨道倾角在90度至180度之间。
* 相对于旋转地球的轨道可视化-地面轨迹移动
为了可视化轨道相对于旋转的地球运动,用一个在地球表面上的位置投影来跟踪航天器。 投影的路径称为地面轨迹(星下点轨迹-航天器和地心连线与地面交点的移动轨迹)。 当卫星绕地球轨道运行时,地面轨迹向西移动有两个原因。 首先,主要因素是地球在轨道平面下向东旋转。 其次,由于地球不是一个均匀的球体,并且在赤道处隆起,其重力在赤道处最大,这导致轨道平面绕地球的极轴缓慢旋转,在运动里称为进动。 对顺行轨道进动向西,对逆行轨道进动向东。
对于低地球轨道,例如在150英里高度 的航天飞机,由于地球自转,地面轨迹向西偏移约22度半,而由于进动引起的偏移仅约半度。
*发射场纬度和地面轨道南北纬度极限
卫星轨道的倾角决定其地面轨道的南北纬度极限,最小轨道倾角等于发射场所处的纬度,并通过向正东方向发射来实现。例如,如果卫星从肯尼迪航天中心向东发射, 它位于北纬28度半,其最小轨道倾角将为28度半,其地面轨迹的范围将在北纬28度半和南纬28度半之间变化。
*发射方位角
如果从正北方向向东测量的发射方位角或飞行方向从正东方向增大,则轨道倾角会增大,并且南北地面轨道的最大纬度会相应增加,从而使地面轨道的纬度极限等于新的发射倾角。
同样,如果发射的方位角从正东减小,轨道倾角也再次增加,地面轨道的 纬度极限也增加。肯尼迪航天中心发射的最大实际倾角为57度,该极限出于安全考虑,为保护航天器和它的助推器系统在上升阶段避开 地面人员。为了获得倾斜度大于57度的轨道,航天器从加利福尼亚范登堡空军基地发射。范登堡基地 提供了向南发射轨道倾角约为70度顺行至138度逆行。
从范登堡号发射的一大优势是能够经济地实现极地轨道,其地面轨道涵盖从北极到南极的所有纬度。
*地球自转速度增益
地球不断旋转,其表面上的所有点都具有向东速度,最大速度发生在赤道。
发射地点离赤道越远,或者随着发射方位角从正东增加或减小,地球的旋转速度被赋予运载火箭就会越小,这将需要更多的燃料才能进入轨道,或者有效载荷重量必须减少 。从赤道或近赤道向正东发射(例如欧洲航天局用的法属圭亚那的库鲁发射场),欧洲航天局获得大约1500英尺/秒的自由速度增益优势,相比之下,在更北纬的肯尼迪航天中心,可获得每秒大约为1300英尺的增益
从赤道发射场发射的卫星在有效载荷重量方面及实现赤道轨道所需的燃料量最小化方面具有明显优势。因为许多卫星都在赤道轨道上运行,这些是重要的考虑因素。
*发射窗口
航天器在指定的时间间隔内发射,该时间间隔叫发射窗口。 影响发射窗口的一些因素包括发射轨道的照明条件、太阳角度、有效载荷轨道要求、如果计划交会,交会分段、跟踪和通信要求,以及避免与其他在轨绕行物体的碰撞等等。
定义航天飞机发射窗口的因素之一是发射光照条件,可以通过绘制时间与一年中的日期来说明。 在此图上,我们看到发射场日光和黑暗关系。 较长白天的日子,发生在一年中间的夏季时间。
航天飞机的方便紧急着陆场如果需要日光条件,则发射窗口现在看起来像这样。 在冬季月份,仅照明条件有效发射窗口就可以小至三小时,考虑其他诸多条件,可用发射窗口变得更加受限。
*运载火箭
用于执行任务的特定运载工具的选择取决于有效载荷的重量、大小、以及所需的轨道。用于将航天器发送到轨道上的消耗性火箭通常包括数级,可同时包含固体和液体推进剂进行推进。当每级的燃料耗尽时,用过的级被抛弃。分级可提供不再需要时丢弃重量的好处。
*轨道器操纵系统
航天飞机是一个两级系统,在升空时,两个固体火箭助推器和三个航天飞机主发动机同时产生推力。飞行大约两分钟后,在25英里的高度上,燃料和固体火箭助推器被耗尽,被抛弃。然后以外挂油箱中携带的液氧和液氢为燃料的三个主发动机继续燃烧几分钟,直到航天飞机达到其截止速度,此时主发动机关闭, 将外挂油箱抛弃。最后需要使用称为“欧姆”的轨道器操纵系统再进行两次燃烧,才能将轨道器置于其最终轨道。 在主机关闭大约两分钟后,欧姆就燃烧了一次,并确定了轨道远地点。 欧姆的两次燃烧大约在30分钟后发生,并使轨道圆化
*Delta V
一旦卫星被发射,进入轨道,通常有必要通过在轨燃烧改变轨道, 描述在轨燃烧或发动机点火的常用术语是Delta V。Delta V是燃烧引起的航天器速度变化,单位为英尺/秒,速度变化自于燃烧。燃烧期间所需的燃料量取决需要的Dela V变化量,和航天器的质量。因为所携带的燃料量有限,燃料消耗是航天器任务规划中的主要考虑之一,对轨道寿命至关重要 。
*“顺行燃烧” 和“逆行燃烧”
航天器在轨道上推力可以向任何方向,沿飞行路径向前和向后的燃烧是最常见的。 任何轨道燃烧的唯一特征在于,如果没有其他燃烧,航天器随后将始终再次穿过燃烧点。向前燃烧提高航天器的速度,并且被称为” 顺行燃烧”,对于顺行燃烧,航天器的飞行路径除燃烧点以外的所有点都抬高;与飞行方向相反的燃烧使飞行器减速,称为“逆行燃烧”。对于逆行燃烧,除燃烧点外,轨道的其他位置点都被降低。Delta V越大,燃烧前和燃烧后的轨道差异就越大。
*霍曼转移
轨道燃烧可以组合到操纵序列中以便更改轨道大小、形状或方位,最常见的操纵序列之一由两次燃烧组成,用于完成同一轨道平面上两个圆形轨道之间的轨道转移。 这种类型的轨道之间最节能的转移是霍曼转移。 霍曼转移实际上是半个椭圆轨道,近地点在一个轨道上,而远地点在另一个轨道上。 燃烧发生在转移轨道的近地点和远地点。 使用霍曼转移可将所需的Delta V值降至最低,因此具有使用最少燃料的优势。霍曼转移转移的缺点是比其他大多数转移需要更长的时间。
转移序列的类型取决于任务和可用的燃料量,例如在时间紧迫的太空救援可能会使用快速转移,而在常规的卫星部署中节省燃料以后使用很重要,这很可能会使用霍曼转移 。
*轨道平面修正
到目前为止讨论的燃烧都在原始轨道平面上进行,并且不影响轨道倾角或节点位置。 在某些情况下,需要更改轨道平面,例如设置交会或将卫星布置到赤道轨道上。
要改变倾角,推力矢量必须与轨道平面成一定角度,而在升交点或降交点处具有与轨道平面垂直的推力分量使轨道平面绕交点线转动,
升交点处的向北平面外推力会增加顺行轨道的倾角,而南向的外推力会减小倾角。 平面外推力需要大量燃料,并且仅在绝对需要时才执行。 例如,使用所有机载推进剂,航天飞机在轨平面变化能力小于三度。 卫星轨道的平面和高度由其设计任务确定,该任务通常包括光学或通信目的的视场要求。
*视场
卫星的视场定义为在任何给定时间从卫星看到的地球表面区域。 高轨道卫星的视场比低轨道卫星的视场大,例如,海拔800海里高的卫星的圆形视场直径约为4,100海里,而一颗200海里高的卫星的圆形视场直径约为2,000海里。 低轨道卫星通常用于摄影和其他类型的地球观测。
*地球同步轨道
位于低倾角圆形轨道上,海拔约19,000,300海里的卫星,其角速度与地球的角速度刚好相等,从地面观察,卫星似乎在经度上保持静止,这样的轨道称为地球同步轨道,用于在他们视场内的任何地面站系统提供连续通信能力。
地球同步轨道的视场是恒定的,并且被限制于赤道南和北约70度的纬度区域,在任何一个极点都不可能通过地球同步轨道进行有效的卫星通信。 但是,由于它们的高度,它们的视场几乎覆盖了半个地球。
*地球静止轨道
倾角为0度的特殊地球同步轨道称为地球静止轨道,其卫星似乎悬挂在地球赤道表面上空的固定点。
*莫尼亚轨道
美国大多数通信卫星都位于地球同步轨道上,提供接近全球范围的通信覆盖。为了在高纬度进行有效的通信,使用莫尼亚轨道(Monia俄语意思闪电),是苏联广泛用于其通信卫星的轨道。 莫尼亚轨道高度偏心, 其远地点接近地球同步轨道高度,并且倾角约63度,卫星在北半球的远地点减速,并在南半球的近地点高速通过,这为其轨道75%的周期提供了北半球通信。在莫尼亚轨道上适当间隔布置几颗卫星可以在北纬提供持续的通信。
*低轨道和太阳同步轨道
导航卫星, 如美国海军的运输系统(transit system)和GPS全球定位系统使用较低的轨道,因此用户可以随时从多个卫星接收信号。另一个经常使用的轨道称为太阳同步轨道,它们利用了由于地球不是理想球体而引起的轨道平面的进动
所有太阳同步轨道都是高度倾斜的逆行轨道,它们以每年一转的速度绕地球极轴向东进动,因为地球太阳光线也以每年一转的速度向东旋转,因此轨道平面相对于地球太阳光线的方向将保持恒定。如果卫星周期与地球自转同步,则它将以固定间隔在同一本地时间经过地球表面的同一点。 太阳同步卫星可确保在同一视场之间存在恒定的太阳角和均匀的照明。诸如美国国防气象卫星和“陆地卫星”为太阳同步卫星,定期对整个地球进行同步成像。
*轨道扰动
除地球对航天器的引力吸引使它在绕地球的轨道上运动,还有其他更小的力会导致航天器偏离其期望的轨道,这些力导致所谓的轨道扰动。用于获得太阳同步轨道的轨道进动是由地球非球形的扰动效应产生的。其他扰动力是太阳、月亮和行星的引力,以及太阳风。太阳风是带电的质子和电子流,它们加热地球大气层并增加大气阻力。
在大多数情况下干扰力可以在航天器和轨道设计中得到补偿,不是主要问题。 如果这些力干扰了轨道太多,可以启动推进器以重新建立其期望的轨道方向或高度,这对于航天器在非常低的高度飞行是特别需要的,在这种情况下大气阻力的影响大,如果不补偿,最终会使航天器将脱离轨道。
*航天器使用寿命
航天器的使用寿命通常受维持其期望轨道的燃料量的限制。当卫星使用寿命结束时,卫星将留在轨道上或脱离轨道重新进入地球大气层时燃烧掉。
*航天飞机返回地球
当航天飞机完成其轨道任务后重新进入地球大气层时,它将执行精确的逆行燃烧以启动受控返回地球的过程,该燃烧发生在离着陆场约半个地球路上。逆行燃烧产生的新轨道在离着陆场约四千英里处使轨道器进入地球大气。在此期间轨道器从其轨道高度下降到大气再入,其高度由位于轨道器头部和尾部的反应控制发动机来维持。
轨道器进入地球大气层后,其机翼和尾翼的三角表面将开始发挥作用,逐渐取代喷气姿态控制。 当轨道器接近着陆场时,它会以17至19度的角度长直线方向接近着陆场。 接近跑道时,它会执行机头机动以降低其下沉速度,并以每小时约230英里的速度滑落触地。 随着轨道飞行器停止转动,我们的轨道力学世界的旅程也随之结束。 这只是对行星和卫星运动进行复杂研究的轨道力学基础。








